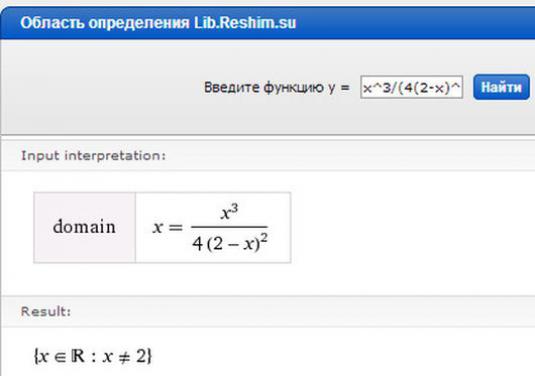
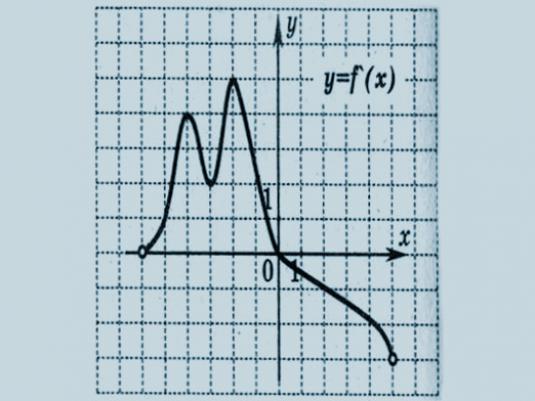
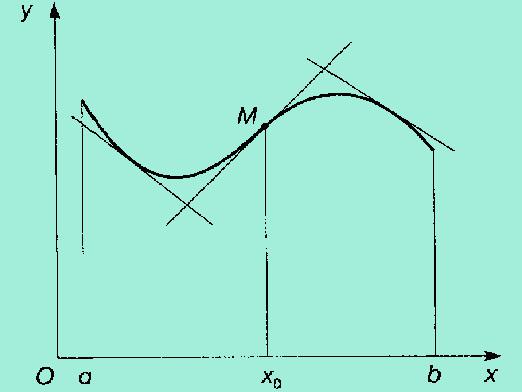
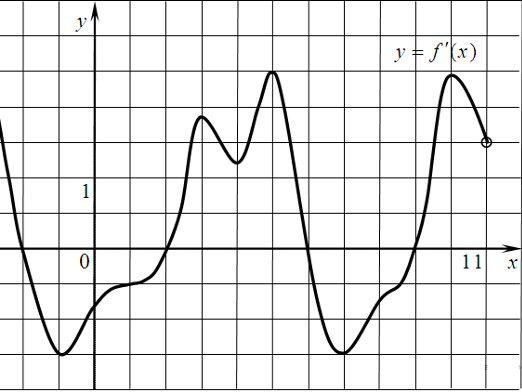
Hvordan finder man derivatet?

Problemet med at finde et derivat af en given funktioner et af hovedkurserne i matematik i gymnasiet og i videregående uddannelser. Det er umuligt fuldt ud at undersøge en funktion, at konstruere sin graf uden at tage dens derivat. Derivat af en funktion kan let findes ved at kende de grundlæggende regler for differentiering, såvel som tabellen over derivater af de grundlæggende funktioner. Lad os finde ud af, hvordan man finder derivatet af en funktion.

En afledningsfunktion er grænsen for forholdet mellem forøgelsen af en funktion og forøgelsen af argumentet, når stigningen af argumentet har tendens til at være nul.

Det er ret vanskeligt at forstå denne definition, daBegrebet grænser er ikke fuldt ud studeret i skolen. Men for at finde derivaterne af forskellige funktioner er det ikke nødvendigt at forstå definitionen, lad os overlade det til matematikernes specialister og gå direkte til at finde derivatet.

Processen med at finde et derivat kaldes differentiering. Når funktionen differentieres, får vi en ny funktion.

Til deres betegnelser vil vi bruge de latinske bogstaver f, g osv.

Der er mange forskellige notater for derivater. Vi vil bruge stroke. For eksempel betyder g "at vi vil finde derivatet af g.

Tabellen over derivater

For at besvare spørgsmålet, hvordan man finderderivat, er det nødvendigt at bringe tabellen over derivater af de grundlæggende funktioner. For at beregne derivaterne af elementære funktioner er det ikke nødvendigt at udføre komplekse beregninger. Det er nok bare at se dets værdi i derivatortabellen.

C "= 0
(sin x) "= cos x
(Cos x) "= -sin x
(xⁿ) "= n x^n-1
(e^x) "= e^x
(ln x) "= 1 / x
(en^x) "= a^xln a
(log_enx) "= 1 / x ln a
(tan x) "= 1 / cos²x
(ctg x) "= - 1 / sin²x
(arcsin x) "= 1 / √ (1-x²)
(arccos x) "= - 1 / √ (1-x²)
(arctg x) "= 1 / (1 + x²)
(arcctg x) "= - 1 / (1 + x²)

Eksempel 1. Find derivatet af funktionen y = 500.

Vi ser at dette er en konstant. Ifølge tabellen over derivater er det kendt, at derivatet af konstanten er nul (formel 1).

(500) "= 0

Eksempel 2. Find derivatet af funktionen y = x¹⁰⁰.

Dette er en effektfunktion i eksponenten, hvoraf 100 og for at finde dens derivat skal man multiplicere funktionen af eksponenten og formindske med 1 (formel 3).

(x¹⁰⁰) "= 100 x⁹⁹

Eksempel 3. Find derivatet af funktionen y = 5^x

Dette er en eksponentiel funktion, vi beregner dets derivat med formlen 4.

(5^x) "= 5^xLN5

Eksempel 4. Find derivatet af funktionen y = log₄x

Afledet af logaritmen findes fra formlen 7.

(log₄x) "= 1 / x ln 4

Differentieringsregler

Lad os nu finde ud af, hvordan man finderAfledt af funktionen, hvis den ikke er i tabellen. De fleste af de undersøgte funktioner er ikke elementære, men er kombinationer af elementære funktioner ved hjælp af de enkleste operationer (tilføjelse, subtraktion, multiplikation, division og multiplikation med et tal). For at finde deres derivater skal man kende reglerne for differentiering. Desuden betegner bogstaverne f og g funktionerne, og C er en konstant.

1. Den konstante koefficient kan tages som tegn på derivatet

(Cf) "= Cf"

Eksempel 5. Find derivatet af funktionen y = 6 * x⁸

Vi tager den konstante koefficient 6 og differentierer kun x⁴. Dette er en effektfunktion, hvis derivat er fundet fra formel 3 i derivatortabellen.

(6 * x⁸) "= 6 * (x⁸) "= 6 * 8 * x⁷= 48 * x⁷

2. Derivatet af en sum er lig med summen af derivaterne

Derefter:

(f + g) "= f" + g "

Eksempel 6. Find derivatet af funktionen y = x¹⁰⁰+ sin x

Funktionen er summen af to funktioner, hvis derivater kan findes fra bordet. Siden (x¹⁰⁰) "= 100 x⁹⁹ og (sin x) "= cos x. Derivatet af summen vil svare til summen af disse derivater:

(x¹⁰⁰+ sin x) "= 100 x⁹⁹+ cos x

3. Derivatet af forskellen er lig med differencen af derivaterne

(f - g) "= f" - g "

Eksempel 7. Find derivatet af funktionen y = x¹⁰⁰ - cos x

Denne funktion er forskellen på tofunktioner, hvis derivater vi også kan finde fra bordet. Derefter er derivatet af forskellen lig med differensen af derivaterne, og vi vil ikke glemme at ændre tegnet, da (cos x) "= - sin x.

(x¹⁰⁰ - cos x) "= 100 x⁹⁹ + sin x

Eksempel 8. Find derivatet af funktionen y = e^x+ tg x-x².

I denne funktion er der en sum og en forskel, vi finder derivaterne af hvert udtryk:

(e^x) "= e^x, (tg x) "= 1 / cos²x, (x²) "= 2. Derefter er derivatet af den oprindelige funktion lig med:

(e^x+ tg x-x²) "= e^x+ 1 / cos²x -2 x

4. Derivat af et arbejde

(f * g) "= f" * g + f * g "

Eksempel 9. Find derivatet af funktionen y = cos x * e^x

For at gøre dette finder vi først derivatet af hver faktor (cos x) "= - sin x og (e^x) "= e^x. Nu erstatter vi alt i produktformlen. Vi multiplicerer derivatet af den første funktion med det andet og tilføjer produktet af den første funktion til derivatet af det andet.

(cos x * e^x) "= e^xcos x - e^x* sin x

5. Derivatet af en bestemt

Derefter:

(f / g) "= f" * g - f * g "/ g²

Eksempel 10. Find derivatet af funktionen y = x⁵⁰/ sin x

For at finde kvotientens derivat finder vi først tælleren og nævnerens derivat separat: (x⁵⁰) "= 50 x⁴⁹ og (sin x) "= cos x. Ved at erstatte kvotientens derivat ind i formlen får vi:

(x⁵⁰/ sin x) "= 50x⁴⁹* sin x - x⁵⁰* cos x / sin²x

Afledt af en kompleks funktion

En kompleks funktion er en funktion repræsenteret ved sammensætningen af flere funktioner. For at finde derivatet af en kompleks funktion er der også en regel:

(u (v)) "= u" (v) * v "

Lad os finde ud af, hvordan man finder derivatet af en sådan funktion. Lad y = u (v (x)) være en kompleks funktion. Vi kalder funktionen u ekstern, og v - intern.

For eksempel:

y = sin (x³) er en kompleks funktion.

Så y = sin (t) er en ydre funktion

t = x³ - internt.

Lad os prøve at beregne derivatet af denne funktion. Med formlen er det nødvendigt at formere derivaterne af de interne og eksterne funktioner.

(sin t) "= cos (t) er derivatet af den eksterne funktion (hvor t = x³)

(x³) "= 3x²er afledt af den indre funktion

Derefter (synd (x³)) "= cos (x³) * 3x²er derivatet af en sammensat funktion.

Læs mere: