Hvordan finder man en sinus, hvis cosinus er kendt?

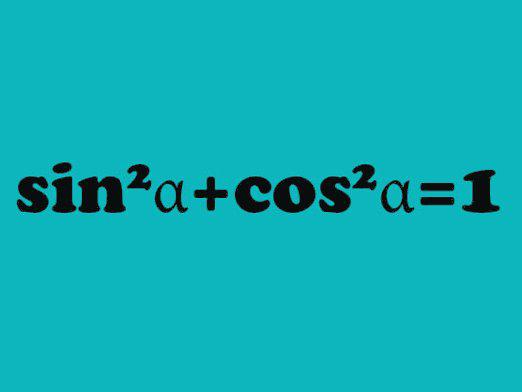
Når der er givet et problem i hvilken en er kendttrigonometrisk funktion, og det er nødvendigt at finde en anden trigonometrisk funktion, det er ikke svært at løse det. Men det er meget vigtigt at tage højde for de små finesser i løsningen. Overvej de detaljerede løsninger i lyset af nuancerne. Der er flere varianter af problemer, hvor det er nødvendigt at finde en sinus, hvis cosinus er kendt.

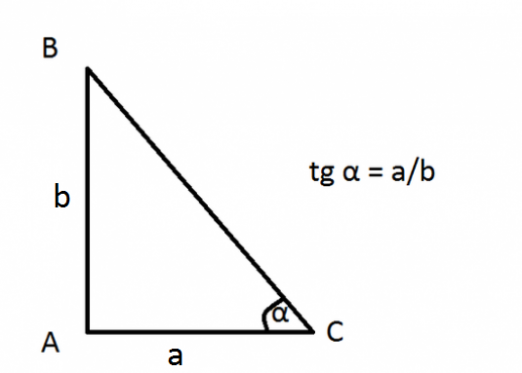
Variant 1. Der gives en rektangulær trekant. Cosinus af vinklen på denne trekant (ikke den rigtige vinkel) er kendt. Nastya er en sinus.

opløsning:

Husk den grundlæggende trigonometriske identitet: synd²a + cos ²a = 1.

Derfor synd²a = 1 - cos²α.

synd a = ± √ (1 cos²α)

I en retvinklet trekant kan værdien af ​​vinklen (ikke direkte) ligge i området fra 1⁰ op til 89⁰. Sinnet af en sådan vinkel er altid positiv, derfor før roden vil vi have et plus.

Variant 2. Cosinus af en vis vinkel er kendt. Det er også kendt, hvilket kvartal af den trigonometriske cirkel vinklen tilhører.

opløsning:

synd²a + cos ²a = 1.

synd²a = 1 - cos²α.

synd a = ± √ (1 cos²α)

Det er kendt, at den trigonometriske funktion er sinuskan tage værdier fra -1 til +1. Derfor skal vi tage højde for dette ved udvindingen af ​​roden. Afhængigt af hvilket kvartal vinklen tilhører, læg et tegn foran roden "+" eller "-".

Hvad er kvartalerne:

• I (først) - α fra 0⁰ op til 90⁰;
• II (anden) - α fra 90⁰ op til 180⁰;
• III (tredje) - α fra 180⁰ op til 270⁰;
• IV (fjerde) - a fra 270⁰ op til 360⁰.

Hvis vinklen tilhører det første eller andet kvartal, så sætter vi ikke roten "-" før tegnet, da i dette tilfælde er sin a altid positiv.

Hvis vinklen tilhører det tredje eller fjerde kvartal, så før rotte tegnet sætter vi "-", da i dette tilfælde er sin a altid negativ.

Et eksempel. På baggrund af cosinus finder du sinus. cos a = v3 / 2. Vinkel i fjerde kvartal.

opløsning:

Så hvordan man finder sinusen, ved at kende cosinusen:

synd a = ± v (1 cos²α)

Siden ved antagelsen af ​​problemet hører vinklen til det fjerde kvartal af den trigonometriske cirkel, sætter vi tegnet "-" før roden.

synd a = -v (1-3 / 4)

synd a = - 1/2.

Et eksempel. I en rektangulær trekant er cosinusen af ​​en vinkel 1/2. Find sinus af denne vinkel.

Løsning: synd²a + cos ²a = 1.

synd²a = 1 - cos²α.

Da vi leder efter vinklen på en retvinklet trekant, tegner "+" foran roden.

synd a = v (l-cos²α)

synd a = v (1-1 / 4)

synd a = v3 / 2.