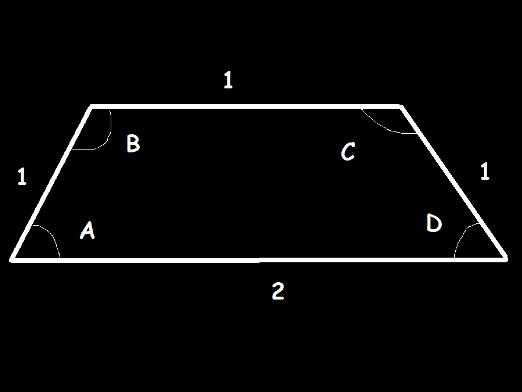
Hvordan finder man vinklerne af en trapezoid?

Trapezoid er en geometrisk figur, en firkant, der har to parallelle linjer. Andre to linjer kan ikke være parallelle, i hvilket tilfælde det ville være et parallelogram.

Typer af trapezier

Trapezier er af tre typer: rektangulære, når de to trapezformede vinkler er 90 grader; Equilateral, hvor de to sidelinier er ens; alsidige, hvor sidelinierne er forskellige i længden.

Arbejde med trapezoer, du kan lære at beregne deres område, højde, linjestørrelse og også for at forstå, hvordan man finder vinklerne i en trapezoid.

Rektangulær trapezoid

Det rektangulære trapezium har to vinkler på 90grader. Summen af ​​de andre to vinkler er 180 grader. Derfor er der en måde at finde vinklerne af en rektangulær trapezform på, idet man kender størrelsen på et af hjørnerne. Lad det være for eksempel 26 grader. Bare brug for fra den samlede mængde trapezformede vinkler - 360 grader - trækker summen af ​​kendte hjørner af. 360- (90 + 90 + 26) = 154. Den ønskede vinkel vil være 154 grader. Det kan betragtes som enklere: da de to hjørner er lige, så i summen bliver de 180 grader, det vil sige halv 360; summen af ​​de indirekte vinkler vil også være 180, så du kan tælle det lettere og hurtigere 180 -26 = 154.

Den ensidige trapezoide

En ligesindet trapezoid har to lige sider, som ikke er baser. Der er formler, der forklarer, hvordan man finder vinklerne af en ligemæssig trapezform.

Beregning 1, hvis dimensionerne af siderne af trapezoidet er givet

De betegnes med bogstaverne A, B og C: A - Dimensioner af siderne, B og C - henholdsvis basisens dimensioner, mindre og større. Trapezen skal også kaldes ABCD. Til beregninger er det nødvendigt at tegne højden H fra vinklen B. En rektangulær trekant BHA blev dannet, hvor AH og BH er katoder, AB er hypotenusen. Nu er det muligt at beregne størrelsen af ​​AN-kurven. For at gøre dette er det nødvendigt at trække den mindre fra den større trapezformede base og dele den i halve; (c-b) / 2.

For at finde den akutte vinkel på en trekant,brug cos-funktionen. Cos af den nødvendige vinkel (β) vil være lig med a / ((c-b) / 2). For at finde størrelsen af ​​vinklen β, er det nødvendigt at bruge funktionen arcos. β = arcos 2a / c-b. fordi de to vinkler af en ligesidet trapezium er ens, de vil være: vinkel BAD = vinkel CDA = arcos 2a / c-b.

Dernæst skal du finde ud af, hvordan du finder de trapezformede vinkler, der er tilbage. Det er nemt nok. Vinkel ABC = vinkel BCD = 360 - 2x (arcos 2a / c-b) = 180 - arcos 2a / c-b.

Beregning 2. Hvis dimensionerne af baserne af trapezoidet er givet.

At have værdierne for baserne af trapezoidet - a og b,Brug samme metode som i den foregående løsning. Fra vinklen b skal højden h være faldet. Har dimensionerne af de to ben i trekanten lige oprettet, kan du bruge en lignende trigonometrisk funktion, kun i dette tilfælde vil det være tg. For at konvertere vinklen og få dens værdi, skal du bruge funktionen arctg. Når vi opnår formlerne, opnår vi størrelsen af ​​de nødvendige vinkler:

β = arctg 2h / c-b, og vinklen a = 180 - arctg 2h / c-b /

En almindelig alsidig trapezoid

Der er en måde at finde en større vinkel på trapeziet på. For dette er det nødvendigt at kende dimensionerne af begge akutte vinkler. At kende dem og vide, at summen af ​​vinklerne på en hvilken som helst base af trapezoiden er 180 grader, konkluderer vi, at den ønskede stump vinkel vil bestå af en forskel på 180 - størrelsen af ​​den akutte vinkel. Du kan også finde en anden uklar vinkel af trapeziet.