Hvordan finder man hældningen?

I matematik beskriver et af parametrenepositionen af linjen på det kartesiske koordinatplan er hældningen af denne linje. Denne parameter karakteriserer hældningen af den lige linje til aksen af abscissen. For at forstå hvordan man finder vinkelkoefficienten, husker vi først den generelle form af ligningens ligning i XY-koordinatsystemet.
Generelt kan enhver linje repræsenteres af udtrykket ax + ved = c, hvor a, b og c er vilkårlig reelle tal, men en2 + b2 ≠ 0.
En lignende ligning ved hjælp af simpletransformationer kan bringes til formen y = kx + d, hvor k og d er reelle tal. Tallet k er en vinkelkoefficient, og ligningen af en lige linje af denne art kaldes en ligning med en vinkelkoefficient. Det viser sig, at for at finde vinkelkoefficienten behøver du bare at bringe den oprindelige ligning til ovenstående formular. For en mere fuldstændig forståelse, overvej et bestemt eksempel:
Problem: Find den vinkelmæssige koefficient af linien defineret ved ligningen 36x - 18y = 108
Løsning: Vi transformerer den oprindelige ligning.
36x - 18y = 108
18y = 36x - 108
y = 2x - 6
Svar: Den nødvendige vinkelkoefficient på denne linje er 2.
Hvis vi i løbet af transformationer af ligningen vifik et udtryk for type x = const og kan derfor ikke repræsentere y som en funktion af x, så har vi en lige linje parallelt med X-aksen. Vinkelkoefficienten for en sådan linje er lig med uendelig.
For linjer, der udtrykkes af en ligning af typen y = const, er hældningen nul. Dette er typisk for lige linjer parallelt med abscissaeaksen. For eksempel:
Problem: Find hældningen af linjen givet af ligningen 24x + 12y - 4 (3y + 7) = 4
Løsning: Vi reducerer den oprindelige ligning til den generelle form
24x + 12y - 12y + 28 = 4
24x = 28 - 4
x = -1
Det er umuligt at udtrykke y fra det resulterende udtryk, derfor er hældningen af den givne linje lig med uendelig, og linjen selv vil være parallel med Y-aksen.
Geometrisk betydning
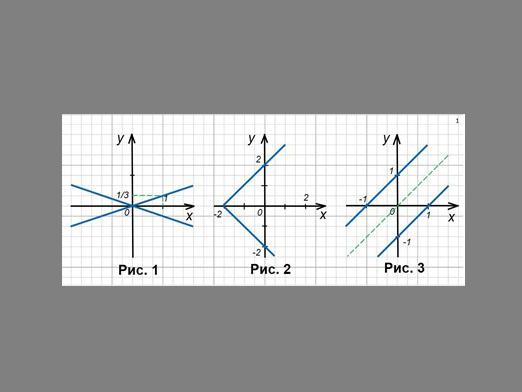
For en bedre forståelse, lad os se på billedet:

I figuren ses en graf af en funktion af typen y = kx. For nemheds skyld tager vi koefficienten c = 0. I trekanten OAB er forholdet mellem BA og AO's side lig med vinkelkoefficienten k. På samme tid er forholdet BA / AO tangentet for den akutte vinkel a i den retvinklede trekant OAB. Det viser sig, at vinkelkoefficienten for den lige linje er lig med vinkelsangens tangent, hvilket er denne linje med aksen af abscissen af nettet.
Løsning af problemet, hvordan man finder hældningendirekte finder vi tangent vinklen mellem den og x-aksen i koordinatnettet. Grænseværdierne, når den pågældende lige linje er parallel med koordinatakserne, bekræft ovenstående. For den lige linje, der beskrives af ligningen y = const, er vinklen imellem den og aksen af abscissen nul. Nulpunktets tangent er også nul, og hældningen er også nul.
Til lige linjer vinkelret på abscissens akse ogbeskrevet af ligningen x = const, vinklen mellem dem og X-aksen er 90 grader. Tangentet af en ret vinkel er lig med uendeligheden, så vinkelkoefficienten af sådanne linjer er lig med uendelighed, hvilket bekræftes af det, der er skrevet ovenfor.
Tangentets vinkelkoefficient
Fælles, fælles ompraksis, er opgaven også at finde tangentens vinkelkoefficient på grafen af funktionen på et tidspunkt. Tangentlinjen er en lige linje, derfor er begrebet vinkelkoefficient også anvendelig for den.
For at forstå, hvordan man finder hældningentangential, vi skal huske begrebet derivat. Derivatet af en hvilken som helst funktion på et tidspunkt er konstant numerisk lig med tangenten af den vinkel, der dannes mellem tangenten på det angivne punkt til grafen for denne funktion og abscissasaksen. Det viser sig at bestemme tangentens vinkelkoefficient ved punktet x0, skal vi beregne værdien af derivatet af den oprindelige funktion på dette punkt k = f "(x0). Overvej eksemplet:
Problem: Find hældningen af linjen tangent til funktionen y = 12x2 + 2xex ved x = 0,1.
Løsning: Vi finder derivatet af den oprindelige funktion i den generelle form
y "= 24x + 2xex + 2ex , så erstatter vi værdien x -
y "(0,1) = 24. 0,1 + 2. 0,1. e0,1 + 2 .e0,1
y "(0,1) = 4,831
Svar: Den nødvendige vinkelkoefficient ved punktet x = 0,1 er 4.831