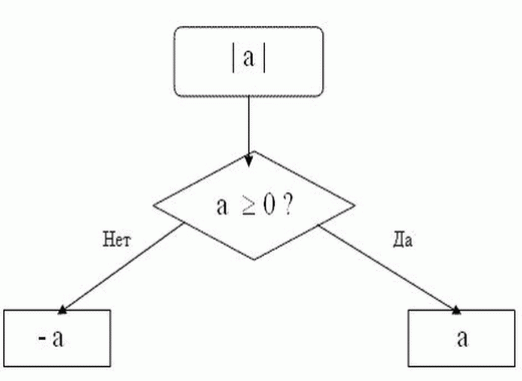
Hvordan løses moduler?

Et modul er absolutværdien af et udtryk. På en eller anden måde udpege et modul, er det almindeligt at bruge direkte parenteser. Den værdi, der er omsluttet i lige parenteser, er den værdi, der tages i modul. Processen med at løse et hvilket som helst modul består i at afsløre de samme lige parenteser, der kaldes modulære parenteser i matematisk sprog. Deres oplysning sker i henhold til et vist antal regler. Også for at løse moduler er der også værdisæt af de udtryk, der var i modulære parenteser. I de fleste tilfælde udvides modulet på en sådan måde, at udtrykket, der var submodulært, modtager både positive og negative værdier, herunder nul. Hvis vi starter fra de etablerede egenskaber af modulet, kompileres forskellige ligninger eller uligheder fra det oprindelige udtryk i processen, som derefter skal løses. Lad os se på, hvordan man løser moduler.
Løsningsproces
Modulets løsning begynder med optagelsen af originalenligninger med modul. For at besvare spørgsmålet om, hvordan man løser ligninger med et modul, skal du åbne det helt. For at løse en sådan ligning afsløres modulet. Alle modulære udtryk skal overvejes. Det skal bestemmes ved hvilke værdier af de ukendte mængder, der udgør sammensætningen, og det modulære udtryk i parentes vender til nul. For at gøre dette er det nok at ligne udtrykket i modulære parenteser til nul, og derefter beregne løsningen af den resulterende ligning. De fundne værdier bør fastsættes. På samme måde skal vi også bestemme værdien af alle de ukendte variabler for alle modulerne i den givne ligning. Dernæst skal vi tage fat på definitionen og overvejelsen af alle tilfælde af eksistens af variabler i udtryk, når de er forskellige fra nul. For at gøre dette skal vi skrive ned et system af uligheder henholdsvis til alle modulerne i den oprindelige ulighed. Ujævnheder skal udformes således, at de dækker alle tilgængelige og mulige værdier for en variabel, der findes på en talelinie. Derefter skal du tegne denne meget numeriske linje til visualisering, hvor i fremtiden udsætte alle modtagne værdier.
Næsten alting kan nu gøres på internettet. Modulet er ikke en undtagelse fra reglerne. Løs online kan det være på en af de mange moderne ressourcer. Alle de værdier af variablen, der er i det zeroth-modul, vil være en speciel begrænsning, der vil blive anvendt i processen med at løse modulære ligninger. I den indledende ligning er det nødvendigt at åbne alle tilgængelige modulære bøjler, mens du ændrer tegnet på udtrykket, så værdierne for den krævede variabel falder sammen med de værdier, der er synlige på nummerlinjen. Den resulterende ligning skal løses. Værdien af variablen, der vil blive modtaget under ligningens opløsning, skal kontrolleres for en begrænsning, som er angivet af selve modulet. Hvis værdien af variablen fuldt ud opfylder betingelsen, så er den korrekt. Alle de rødder, der vil opnås under ligningens opløsning, men ikke vil blive nærmet af begrænsninger, skal kasseres.
Eksempelopløsning: