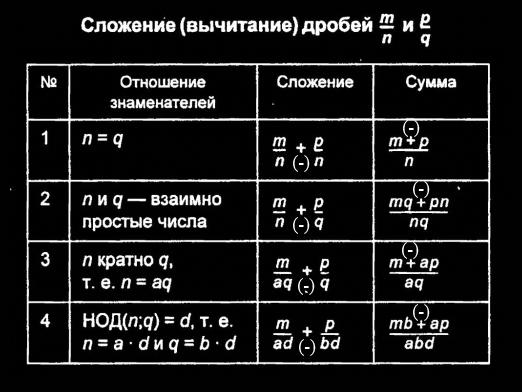
Hvordan finder du fraktioner?

Matematik er dronningen af videnskaber. Hendes storhed er uendelig, men hendes magt er stor. Alle andre videnskaber er afhængige af matematiske resultater. Uanset om det er fysik, kemi, biologi og endda filologi.
Da huset består af mursten, så er der i hver opgave små undertekster. Og ved at lære at løse små, kan du lære at løse mere komplekse problemer.
I dag analyserer vi hvordan man finder fraktioner. Begrebet fraktioner opstod i det antikke Grækenland, efter at grækerne introducerede begrebet længde, svarende til heltal. Dernæst havde vi brug for et koncept, der udtrykker en del af længden, for eksempel halvdelen, en tredjedel af længden. Så syntes begrebet fraktion.
Sætet af rationelle tal Q er sættet af tal repræsenteret i form m / n, hvor m, n er heltal. Nummeret m / n hedder en almindelig fraktion, hvor m er en tæller, og n er en nævner, n ≠ 0.
Hvis n = 〖10〗 ^ k, k = 1,2, ..., så er en sådan fraktion kaldet decimal og skrevet som 0,0..0m, med antallet af nuller, når kommaet er k-1.
Et tal siges at være sammensat, hvis det har andre divisorer udover 1 og sig selv.
Grundlæggende operationer
Fraktioner kan tilføjes, subtraheres, multipliceres, deles, hæves til en effekt. Disse operationer er grundlæggende. I eksemplerne
Vi vil flytte fra simpelt til komplekst og vise eksempler på, hvordan disse eller andre operationer udføres.
Sådan reduceres en brøkdel
For at gøre dette skal vi udvide tælleren og nævneren af primære faktorer, hvis de er sammensatte faktorer. Og hvis disse simple faktorer falder sammen, skal du slette dem.
I fravær af primære faktorer kaldes fraktionen irreducible. For eksempel er 85/65 = (17 * 5) / (13 * 5) = 17/13
Sådan finder du en brøkdel af nummeret
Lad nummeret være en vis længde. En brøkdel er i det væsentlige en del af denne længde, så for at finde heltaldelen multipliceres brøkdelen med tallet. For eksempel er 2/3 af 27 = 27 * 2/3 = 27/3 * 2 = 18
Sådan finder du en brøkdel fra en brøkdel
Faktisk er dette en simpel multiplikationsproces for at finde en brøkdel af en brøkdel, du multiplicerer kun 2 brøker. For eksempel 2/3 og 13/17: 2/3 * 13/17 = 26/51
Fission af fraktioner
Når man deler brøker a / b, c / d, kan divisoren c / d være repræsenteret som d / c og multiplicere, og derefter skåret. For eksempel 27/17? 9/34 = 27/17 * 34/9 = 2 * 3 = 6.
Det er også nødvendigt at huske, at når man løser komplekseksempler skal komme op med en løsningsalgoritme. Det kan være nødvendigt at ændre divisionen i multiplikation med en ændring i brøkdel, det er muligt at udføre multiplikation og division med samme nummer. Sådanne enkle nok instruktioner vil hjælpe med at løse eksempler.
Som et eksempel, tag den klassiske tekstopgave. Fra et lager, hvor der var 150 tons brændselsolie stjålet 2/3. De stjålne dele blev fordelt i dele i forholdet 5/17 og 12/17, sidstnævnte blev transporteret til forarbejdning. Den resterende brændselsolie blev transporteret til forarbejdning. Hvor meget brændselsolie er blevet genanvendt?
150 * 2/3 * 12/17 + 150 * (1-2/3) = 150 * 41/51
Opgaver for fraktioner er grundlaget for skolens aritmetik. De er ikke komplekse i naturen, men det kræver at være flittige og opmærksomme. Hvis disse betingelser er opfyldt, vil resultatet ikke vare lang tid.