Hvordan man skriver en cirkel i en trekant?

Lad os først se på cirklenkan kaldes indskrevet i en trekant. Det er ikke kun for dig at tage og tegne en figur i trekanten. Denne cirkel kan kaldes indskrevet i en trekant, som har tre punkter på buen, der er i kontakt med trekantene af trekanten.
Fra denne definition følger det, at i hvertrekant, kan du kun indtaste en enkelt mulig cirkel, hvis center er ved skæringspunktet mellem tre bisektorer af indvendige vinkler af denne trekant.
Nu mere om, hvordan man skriver en cirkel i en trekant:
- Vi finder trekantens hjørner, som vi husker, tre af dem.
- Fra hvert hjørne er det nødvendigt at tegne cirkler ved hjælp af et kompas og kan være af vilkårlig radius.
- Find nu skæringspunktet for de to cirkler (dette punkt skal være på siden af trekanten, der er modsat det delelige hjørne) og forbinder det delbare hjørne.
- Denne operation skal udføres med hver af de tre hjørner. Du vil ende med tre skærende bisektorer.
- Midtpunktet af cirklen indskrevet i trekanten vil være ved skæringspunktet for sin bisektrix.
- Brug derefter en cirkel med en cirkel med midten på det resulterende punkt.
Sådan indskriver du en trekant i en cirkel
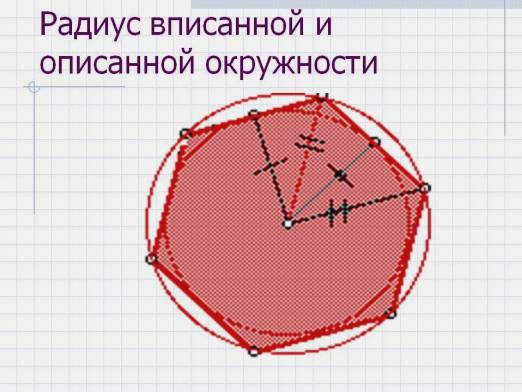
En trekant indskrevet i en cirkel kaldes en trekant, hvis tre hjørner er i kontakt med cirklen. Derefter kaldes cirklen omkredset rundt om trekanten.
Heraf følger, at denne cirkels radius -Dette er segmentet der forbinder midten af den omtalte cirkel og trekanten af trekanten. For at indskrive en trekant i en cirkel er det derfor nødvendigt at angive tre punkter på en cirkel og forbinde dem efter segmenter.