Hvad er den cirkulære cirkels radius?
Se videoen

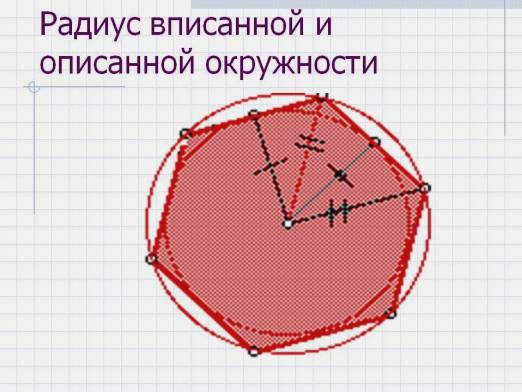
Omkredsen af en polygon, der er beskrevet, er en cirkel, der passerer gennem alle hjørner af en given polygon. Radien beregnes for hvert enkelt tilfælde individuelt.
Hvad er radius af den omkredsede cirkel af en trekant
Formlen for at finde radius af en trekants omkreds er som følger:
- R = abc / 4√p (p-a) (p-b) (p-c),
hvor R er cirkelens radius; a, b, c - sider af trekanten; p er en semiperimeter

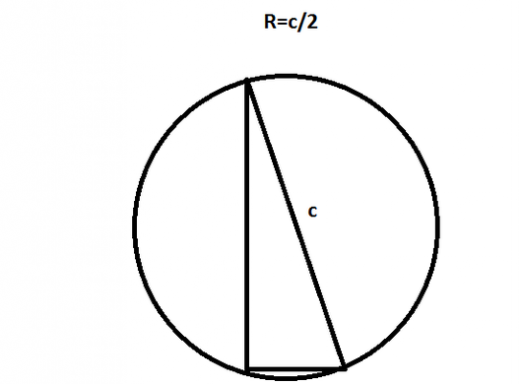
Vi overvejer også det særlige tilfælde, når trekanten er rektangulær.
Radien af cirklen, der er beskrevet nær den højre trekant, beregnes mere simpelt, den er lig med halvdelen af hypotenusens længde:
- R = c / 2.
Beregningen af en cirkels radius i et andet bestemt tilfælde, når trekanten er ligesidet, kan læses i artiklen Sådan finder du radius for den omtalte cirkel.
Dernæst overvejer vi særlige tilfælde og giver formler.
Radien af den omskrevne cirkel af en sekskant
Radius af en sekskants cirkel er lig med længden af en af dets sider eller halvdelen af dens diagonale:

- R = a = d / 2.
Her er a siden af sekskanten, d er dens diagonale.
Radius af den omkredsede cirkel af et ligesidet trapezium
Trapezets omkredsradius beregnes ved hjælp af sider og diagonaler. Formlen er som følger:

- R = adc / 4√p (p-a) (p-d) (p-c),
i dette tilfælde er a, c basis for trapeziet; d er dens diagonale; p - semiperimeter, beregnet ved formlen:
- p = (a + d + c) / 2.
Radius af den omskrevne cirkel af rektanglet
Radien af den cirkel, der er beskrevet nær rektanglet, er lig med halvdelen af dens diagonale eller

- R = √ (a² + b²) / 2 = d / 2.
Radien af den omkredsede cirkel af en firkant
En firkant er et specielt tilfælde af et rektangel, hvor alle sider er lige, så cirkelens radius omkretses om halvdelen af diagonalen:

- R = d / 2.
Du kan også beregne radiusen ved at kende værdien af siden af firkanten: R = a / √2, det vil sige, at radiusen i dette tilfælde er lig med forholdet mellem længden af siden af firkanten og roden af de to.
For at finde andre indikatorer på denne figur, læs også vores artikel Sådan finder du en cirkels diameter | Diameter af den omtalte cirkel.
I geometri er der også begrebet indskrevet cirkel. Til beregning af parametrene i denne figur læses i vores artikel Sådan finder du radius af den indskrevne cirkel.