Hvordan finder man vinklen mellem vektorer?
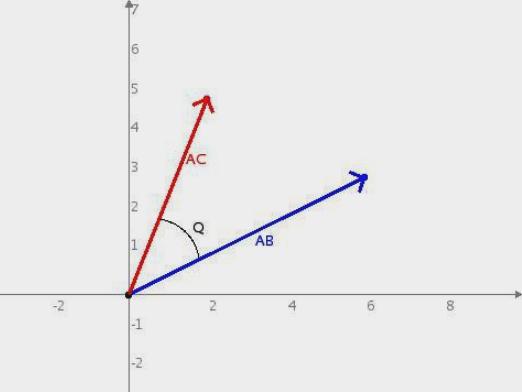
Vinklen mellem de to vektorer, der går medet punkt er den nærmeste vinkel, en rotation hvor den første vektor omkring dens oprindelse vil føre den til positionen for den anden vektor. Men hvordan finder man vinklen mellem vektorerne? Vores artikel vil fortælle om dette.
Vi har to nonzero vektorer, der kommer fra et enkelt punkt - en vektor A med koordinater (x1, y1), vektoren B har koordinaterne (x2, y2). Vinklen mellem dem er μ.
- Vi bruger definitionen af et skalært produkt for at finde graden af vinkeln μ. Vi opnår (A, B) = | A | * | B | * cos (μ). Vi udtrykker cosinus af vinklen. Og så cos (μ) = (A, B) / (| A | * | B |).
- Det kan også findes ved formlen: (A, B) = x1* x2 + y1* y2. Når vektorenes skalære produkt ernul - vektorerne er vinkelrette (vinklen mellem dem er 90 °), så yderligere beregninger udføres ikke. Hvis det skalære produkt har et positivt tegn, er vinklen mellem vektorerne akut, hvis negativt tegn er en stump vinkel.
- Endvidere antager vi, at længderne af vektorerne A og B er givet ved formlerne | A | = v (x1² + y1²), | B | = v (x2² + y2²). Vektørernes længder er de firkantede rødder af summene af kvadraterne af deres koordinater.
- Værdierne af længderne af vektorerne og det skalarprodukt, som findes af dig, er substitueret i formlen opnået fra trin 2, hvilket vil tillade os at finde vinkelsens cosinus. Vi har: cos (μ) = (x1* x2 + y1* y2) / (v (x1² + y1²) + v (x2² + y2²)).
- At have cosinusværdien for at finde vinklen mellemvektorer af, vi bruger Bradys bordet. Også her kan du tage arccosinen. Så opnår vi μ = arccos (cos (μ)). Bradys bordet kan ses, for eksempel her: www.math.com.ua.
For at finde vinklen mellem vektorerne online kan du f.eks. Bruge sådanne links: www.ru.onlinemschool.com og www.mathserfer.com.
Læs mere:

Sådan finder du lydstyrken af en parallelepiped?

Hvordan finder du et firsidigt område?

Hvordan finder man højden på en diamant?
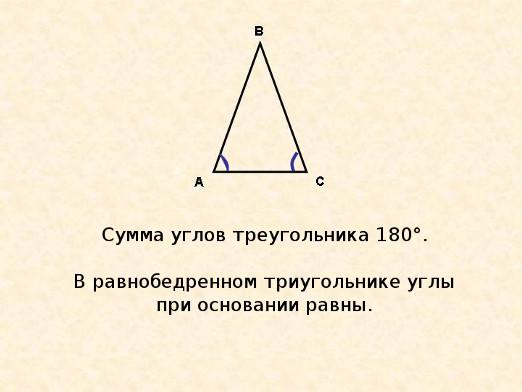
Hvordan finder man vinklerne af en enslig trekant?

Venstre venstre hånd

Hvordan finder man en akkord?
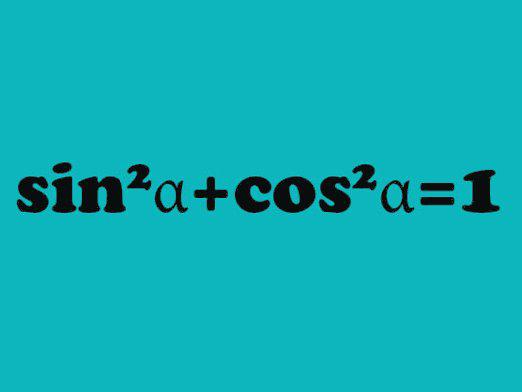
Hvordan finder man en sinus, hvis cosinus er kendt?
Hvordan finder du den cirkulære cirkels radius?

Hvordan finder man katetret?

Hvordan finder man området for et parallelogram?