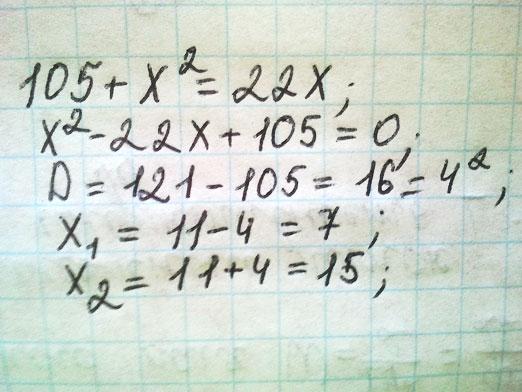Hvordan finder man ligningen af ligningen?

Et af hovedelementerne i matematik er et afsnit, der er dedikeret til at løse ligninger og finde roden i ligninger.

Før du finder roden af ligningen, skal du først finde ud af, hvad det er.

Roten af ligningen er værdien af det ukendteværdier i ligningen betegnet med latinske bogstaver (oftere - x, y, men der kan være andre bogstaver). Dette blev nævnt i vores artikel - Hvad er roden til ligningen.

Overvej hvordan man finder alle rødderne, på forskellige typer af ligninger og specifikke eksempler.

Formuleringen af formen ax + b = 0

Dette er en lineær ligning med en variabel, hvor a og b er tal, og x er roten til ligningen.

Antallet af rødder i ligningen afhænger af værdierne for a og b:

Hvis a = b = 0, så har ligningen et uendeligt antal rødder.
Hvis a = 0, b ikke er 0, har ligningen ingen rødder.
Hvis a ikke er lig med 0, finder vi roden ved hjælp af formlen: x = - (b / a)

eksempel:

5x + 2 = 0
a = 5, b = 2
x = - (2/5)
x = -0,4

Svar: Ruden af ligningen er 0,4

Ligningen er ax2 + bx + c = 0.

Dette er en kvadratisk ligning. Der findes flere måder at finde rødderne i den kvadratiske ligning. Vi vil overveje en generel, der er egnet til at løse for alle værdier af a, b og c.

For det første skal vi finde diskriminanten (D) af denne ligning.

For dette er der formlen:

D = b²-4ac

Afhængigt af hvad diskriminanten har lært, er der 3 muligheder for yderligere løsninger:

Hvis D> 0, rødderne af 2. Og de beregnes ved formlerne:
- x₁= (-b + √ D) / 2a.
- x₂= (-b - √ D) / 2a
Hvis D = 0, så er roden en - den kan findes med formlen: x = - (b / 2a)
Hvis D <0, så har ligningen ingen rødder.

eksempel:

x²+ 3x-4 = 0

Her a = 1, b = 3, c = -4

D = 3² - (4 * 1 * (- 4))
D = 9- (-16)
D = 9 + 16
D = 25

D> 0, så er der 2 rødder i ligningen.

√D = √25 = 5

Vi erstatter alle værdier i vores formel:

x₁ = (-3 + 5) / 2 * 1
x₁= 2/2
x₁= 1
x₂= (-3-5) / 2 * 1
x₂= (-8) / 2
x₂= -4

Svar: Ligningens rødder er 1 og -4.

Formuleringen af form-aksen³+ bx²+ cx + d = 0

Dette er en kubisk ligning.

Der er specielle formler fra Cardano matematikeren, hvorfra man kan løse en sådan ligning, men de er meget komplekse. Vi vil gå den anden, mere forståelige måde.

Kubiske ligninger har altid mindst enroot, og dens værdi er normalt et helt tal fra -3 til 3. Det vil sige, at vi igen vil erstatte i den tilgængelige ligning for x tal: -3, -2, -1, 0, 1, 2 og 3. Dette bliver X_1.

Det er meget enklere og hurtigere end det ser ud til, og helt sikkert nemmere end at bruge Cardano formlerne.

Efter vi finder x₁, gå til søgningen X₂ og X_3.

Til dette formål deler vi vores ligning i (x-x₁) - dette kan gøres ved at lave parenteserne. Vi må have en kvadratisk ligning, som vi løst i denne artikel lidt højere.