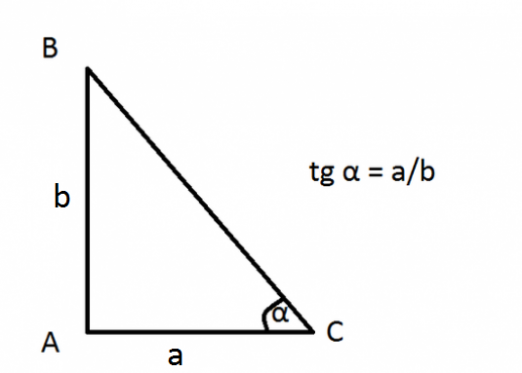
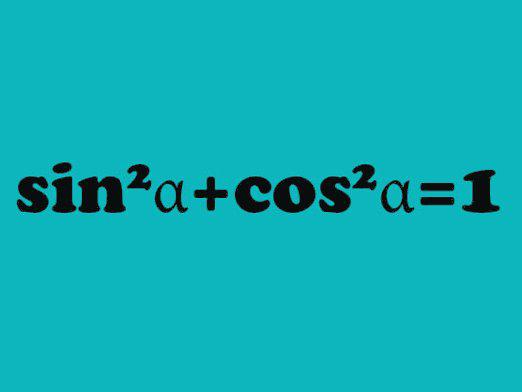Hvordan finder man sinus af en spids vinkel på en trapezoid?

Trapezium er en firkant med to sider parallelt med hinanden. Vi overveje, hvordan man finde sinus spids vinkel trapez, eksemplet trapez ABCD, hvor AD og BC er parallelle sider.
Vi kigger efter sinus af vinklen af en ligesindet trapezform
Overvej et ensartet trapezium. I et ensartet trapezium er siderne ens. I vores tilfælde er AB = CD = 25 og størrelsen af baserne AD = 65 og BC = 51. Lad os prøve at finde sinus af den akutte vinkel.
Som du ved, er sansen lig med forholdet mellem det modsatte ben til hypotenusen, så vi har brug for en rigtig trekant. Vi får det ved at tabe den vinkelrette BH fra hjørnet ABC til bunden.
En vigtig egenskab ved trapezier er dereshøjde - afstanden mellem parallelle sider, som normalt kaldes basen. For at bestemme denne afstand skal du sænke vinkelret på den anden base fra hjørnet af den mindre (normalt øverste) base. I vores tilfælde vil disse være perpendiculars af VN og CE, som vi har brug for at bestemme sinus.
Bestemmelse af trapezens højde
Vi får to rektangulære trekanter, med benene BH = CE og hypotenuse AB = CD. Følgelig er de andre ben af disse trekanter også lig med AH = ED.
Siden i den firkantede HBSE er alle vinkler lige (HB og CE er vinkelret på baserne), så har vi modtaget et rektangel med sider BC = CE.
AD = AH + HE + ED ved konstruktion. Siden AH = ED, og HE = BC, kan denne ligning skrives som:
- AD = 2 * AH + BC.
- AN = (AD - BC) / 2.
Vi erstatter numeriske værdier:
- AN = (65-51) / 2 = 7.
Ved hjælp af Pythagoras sætning søger vi højden af BH:
- AV² = ВН² + АН².
- VN = √ (AV² - AN ²) = √ (25² - 7 ²) = √ (625-49) = √576 = 24
Sådan finder du den trapeziske vinkels sinus
Nu kig efter sinusens akutte vinkel:
- sinBAH = BH / AB.
Vi erstatter numeriske værdier:
- sinBAH = 24/25 = 0,96.
svare:
- sinBAH = 0,96.